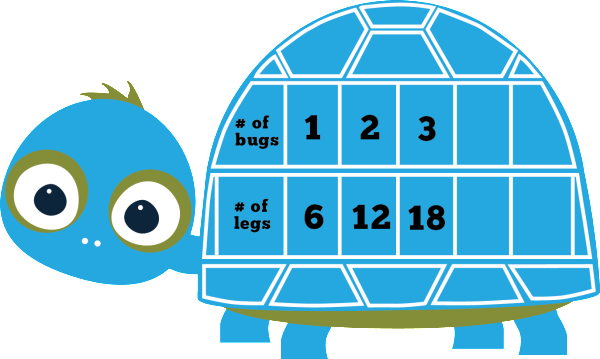
common core problem solving strategies

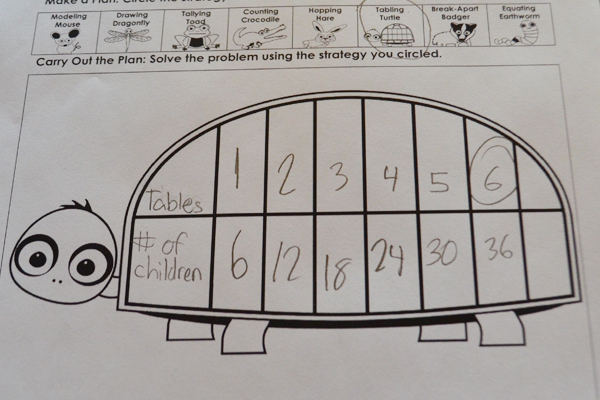
Create Write-On, Wipe-Off Problem-Solving Journals

January 3, 2016By astutehoot

Problem-solving plays an important role in my daily math instruction. Students use pre-made journals to help them complete the problem-solving steps, solve the problem in 2 ways, explain their thinking and rate themselves on a learning scale. These journals track students’ progress with mathematical understanding, strategy selection and application. They also serve as an effective assessment tool. I decided to make a write-on, wipe-off version for students to use during math centers. Follow these 4 easy steps to make them for your classroom, too!

1. Gather materials: You will need a class set of manila folders, problem-solving journal templates, glue sticks, a laminator and dry erase markers.

2. Prepare folders: Glue on the front cover, problem-solving pages on the inside, and the discussion prompts on the back. Laminate and cut out (a perfect job for a parent volunteer).

Journal front 1.5 Inside of problem solving journal Back of problem solving journal mat

3. Select appropriate story problems: I use differentiated story problems during math instruction and color code to keep them organized. An extensive story problem bank is included in our Problem-Solving Essentials Bundle.
Word problems

4. Model procedures and provide practice: Explain how to use the write-on, wipe-off problem-solving journals. Model how to use a dry erase marker to complete the journal. Select a partner to use the discussion prompts, thinking aloud as you go. Practice using the journals during whole group instruction, roving to monitor student understanding. As students demonstrate understanding, incorporate these journals into math center time, either at an adult-led center or an independent math center.

Page 1.5 Inside of journal

Download our Math Intervention Problem-Solving Essentials Bundle for over 200 pages of lessons, activities, worksheets, printables, everything you need for comprehensive problem-solving instruction during math intervention, special education and general education.

Jessica_blog_signature-SMALL

It’s Tom Tabling Turtle!

April 13, 2014March 20, 2015By astutehoot

Howdy, I’m Tom Tabling Turtle and I make tables-
These are columns and rows with numbers and labels.
Always organize your information, is what I say,
So you can discover patterns and relationships in a logical way.

Tom Tabling Turtle is our newest animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Tom’s unit is perfect for general education, special education, RTI and math intervention. Read more about Tom’s strategy below or download the complete unit here.

WHAT is the table strategy? Students make a table complete with labeled columns and rows. The table strategy helps students write information in an organized format, allowing them to easily identify number patterns and relationships.

WHY is the table strategy important? When students make a table, they organize information in a logical way and critically examine data patterns to create a solution.

HOW do I teach the table strategy? When you introduce and practice the strategy, give students a pre-made table. Todd’s turtle shell provides scaffolding with space for labels and organized columns and rows for neat data entry. As students become proficient with the table strategy, teach them to make their own table so they can use this strategy independently without the need for a pre-made table.

WHEN should I use the table strategy? This is an ideal strategy for developing mathematicians who have a solid number sense foundation. It is most effective for repeated addition or multiplication story problems.

Helpful hints:

Use a pre-made table. Young students often lack fine motor skills needed to construct a table, but are perfectly capable of using this strategy. Provide a pre-made table, such as Tom’s turtle shell or a simple table made in Microsoft Word so students can easily input data.

Provide visual support. After teaching students how to construct a table, be sure to write and post directions (along with visual support) in a prominent place during problem-solving time. Students would also benefit from an anchor chart like this one as well.

Presenting Brian Breaking Badger

April 3, 2014March 20, 2015By astutehoot

Hi, I’m Brian Breaking Badger, and I love to break numbers apart.
Separating place value is considered my art!
I break numbers into ones and tens with my teeth,
Then I work with the place value underneath.
I’ll add or subtract the tens, then the ones.
Before you know it, the problem’s all done!

WHAT is breaking apart? Students use place value knowledge to decompose or break each number apart into hundreds, tens and ones. Depending on the problem, students will either add or subtract each place value (first hundreds, then tens, and finally ones). Students will then add or subtract all numbers to solve the problem. Read more about Brian’s strategy below or download the complete unit here.

WHY is breaking apart important? When students use the breaking apart strategy, they are decomposing numbers by place value. This help helps strengthen mental computation, builds number sense and solidifies foundational place value skills. It also serves as an efficient method to double-check solutions as students.

HOW do I teach breaking apart? Teach breaking in isolation first so that students become familiar with the process of decomposing numbers. After proficiency is demonstrated, students can apply this strategy with story problems.

WHEN should I use breaking apart? This is an ideal strategy for developing mathematicians who have a solid place value and number sense foundation. It is most effective to introduce the breaking apart strategy after students are proficient with the hopping strategy since hopping requires place value identification and decomposition skills.

Helpful Hints:

Provide place value and expanded notation practice. Students need a strong place value foundation to decompose or break apart numbers. Provide regular practice through center games and kinesthetic activities. Simple games such as “Race to 100” where students roll dice and add numbers using place value manipulatives are engaging and effective. This game is the perfect addition to weekly math centers.

Act out the problem. Increase students’ understanding of the mathematical context by acting out the story problem. Students also love to show their badger fangs when they break apart the numbers.

Introducing Clark Counting Crocodile

March 3, 2014March 20, 2015By astutehoot

I’m Clark the Counting Crocodile. Use me to help you count.
Start with the largest number, and draw lines for the remaining amount.
Count on for addition, count back for subtraction;
Then circle the answer as your final action.

Clark Counting Crocodile is the second strategy animal in our Problem-Solving Pond: A Common Core Math Strategy Unit. The Problem-Solving Pond was created to help teachers overcome Common Core math challenges and employ problem-solving strategies with confidence and fidelity. Read more about Clark’s strategy below or download the complete unit here.

WHAT is counting?As students build their number sense and fluency, they are able to solve a story problem with counting. In this strategy, students will learn to count on for addition and count back for subtraction using a 100’s chart for support as needed.

WHY is counting important?Counting is a crucial strategy because it helps students explore the relationships and patterns between numbers. Students need to recognize the order of numbers so they can understand that it is more efficient to start with bigger number. For example, in order to solve “4+27,” they should start counting from 27 and progress to “28, 29, 30, 31” instead of starting from 4 and progressing to 31, because in the latter case, they would have to count much more, increasing the possibility of errors. Proficient counting lays the foundation for number sense and place value.

HOW do I teach counting? Explain that Clark helps mathematicians solve problems by counting on to find the total or counting back to find the difference.

Counting on for addition: Students start with largest number in the problem; they put that number in Clark’s mouth and then draw the number of lines for the second number in the problem (if the second number is 14, students would draw 14 lines). Students then label the lines (below the line) and count on, writing each number above the line. Students circle the answer and write equation below to solidify understanding.

Counting back for subtraction: Students start with the largest number in the problem; they put that number in Clark’s mouth and then draw the number of lines for the second number in the problem (if the second number is 14, students would draw 14 lines). Students then label the lines (below the line) and count back, writing each number above the line. Students circle the answer and write equation below to solidify understanding.

WHEN should I use counting? This strategy isideal for problems that include smaller numbers. Most teachers use this strategy with K-2 mathematicians, but this is also beneficial for older students as it works for money, multiplication and division (included in unit).

Helpful Hints:

Create counting bags. Create counting bags with different numbers of objects in each bag and a set of appropriate number cards. Use common manipulatives such as cubes, beans, tiles for bags. Students also love seasonal items such as conversation hearts, acorns, pumpkins, shamrocks, etc. Have student count objects in each bag and then select the number card to name that amount. Students can simply place the objects and number card back into the baggie for checking. Mark the bags with letters or shapes for easy checking of student work.

Provide opportunities for strategy exploration. Allow students to build conceptual understanding by having them solve a counting problem in multiple ways. Students can solve the problem starting with the big number first and double-check solution by starting with the smaller number first. This exploration will guide students to recognize that while it is more efficient to start with the larger number in the problem, number order does not affect the sum. Provide templates with larger numbers; this will help students observe that the counting strategy is not efficient for larger numbers.